1D Filtering

01 May 2025 - 9 mins read time
Tags: computer science programming

Introduction

1D filtering is used in a wide variety of use cases: time series, forecasting, ECC signals, or, as focused here, filtering profiles like those scanned with laser profilometers, where causality (dependency on distant past values) is less critical than spatial contiguity/coherence in neighborhood points, robustness against data loss, extreme outliers, and preservation of central trends.

In this post, we will explore various 1D filtering techniques and apply them (implemented in C++) to two different 1D signals: a C Major chord signal and a real laser-scanned profile. See here the implemented code!

Algorithms

Each subsection combines theory, code, and results. A global visual/quantitative comparison is provided at the end. Later sections will explain filtered signals and how noise was added. First, we briefly describe each method and show visual results.

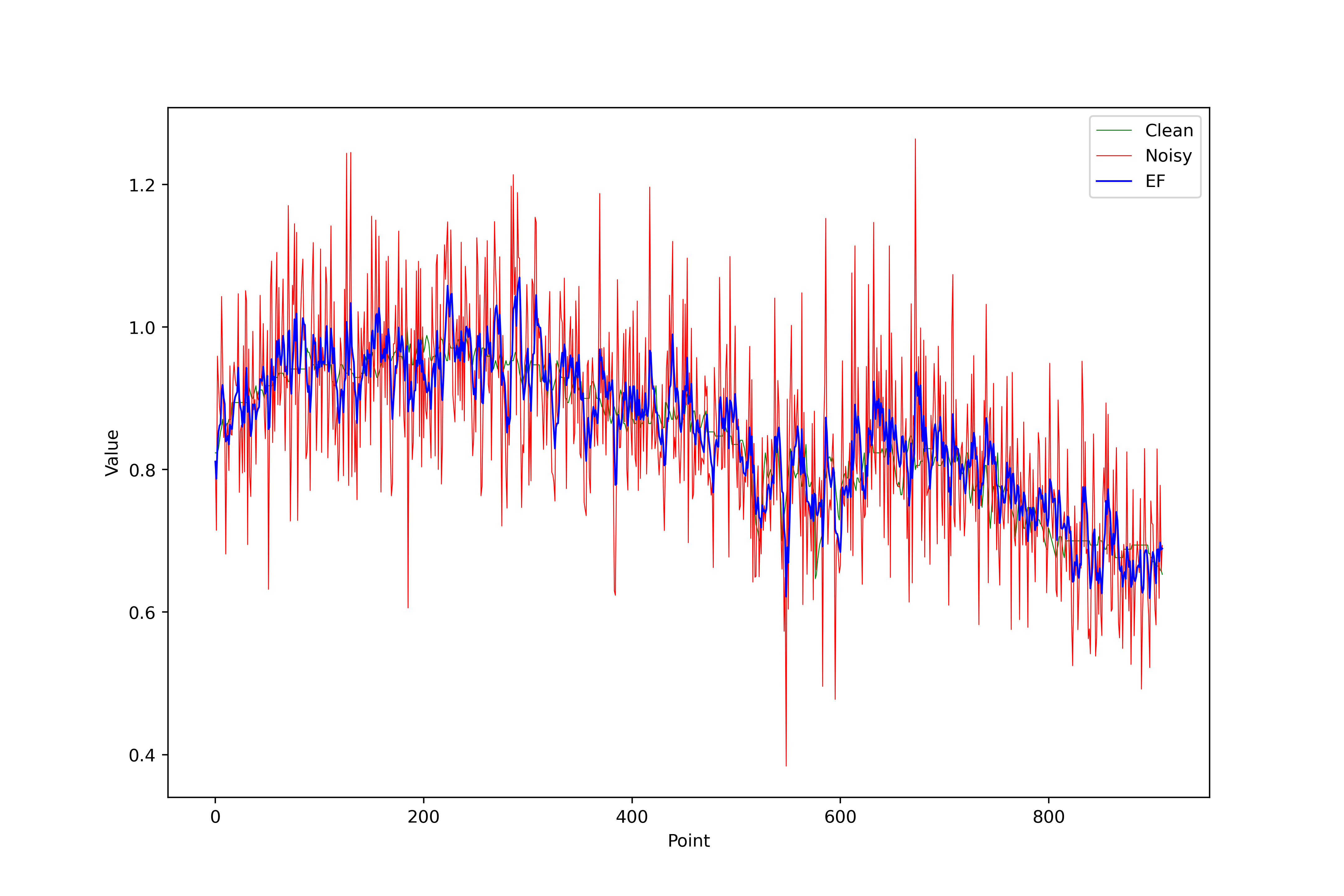
Exponential Filter

Smooths signals by exponentially weighting past values. This filter applies exponential smoothing (aka exponential moving average), commonly used in signal processing for smoothing or creating a “moving average” with emphasis on recent values.

Equation: \(y[i] = \alpha \cdot x[i] + (1 - \alpha) \cdot y[i-1]\)

Parameters:

Filtered Results: EF_CMajor EF_profile

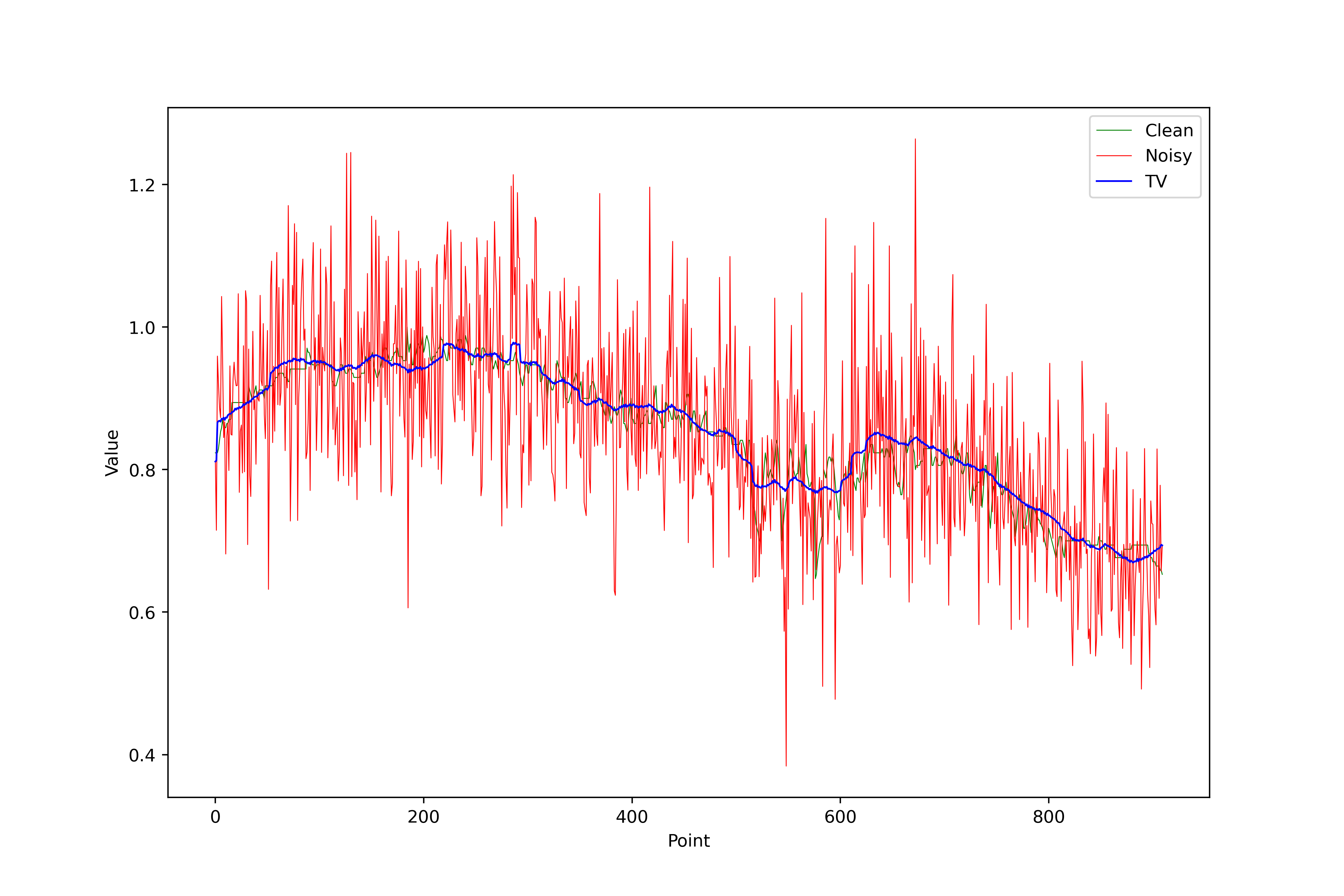
Total Variation (TV) Filter

Minimizes total variation (gradients) while preserving edges.

Energy Minimization Equation: \(y[i] = \alpha \cdot x[i] + (1 - \alpha) \cdot y[i-1]\)

Parameters:

Filtered Results: TV_CMajor TV_profile

Convex Hull Envelope

Computes upper convex hull of points (i, x[i]).

Implicit Equation: \(y[i] = \max \{ f[j] \ | \ (j, f[j]) \text{ lies on the convex hull} \}\)

Parameters: None (depends on signal geometry)

Filtered Results: CHULL_CMajor CHULL_profile

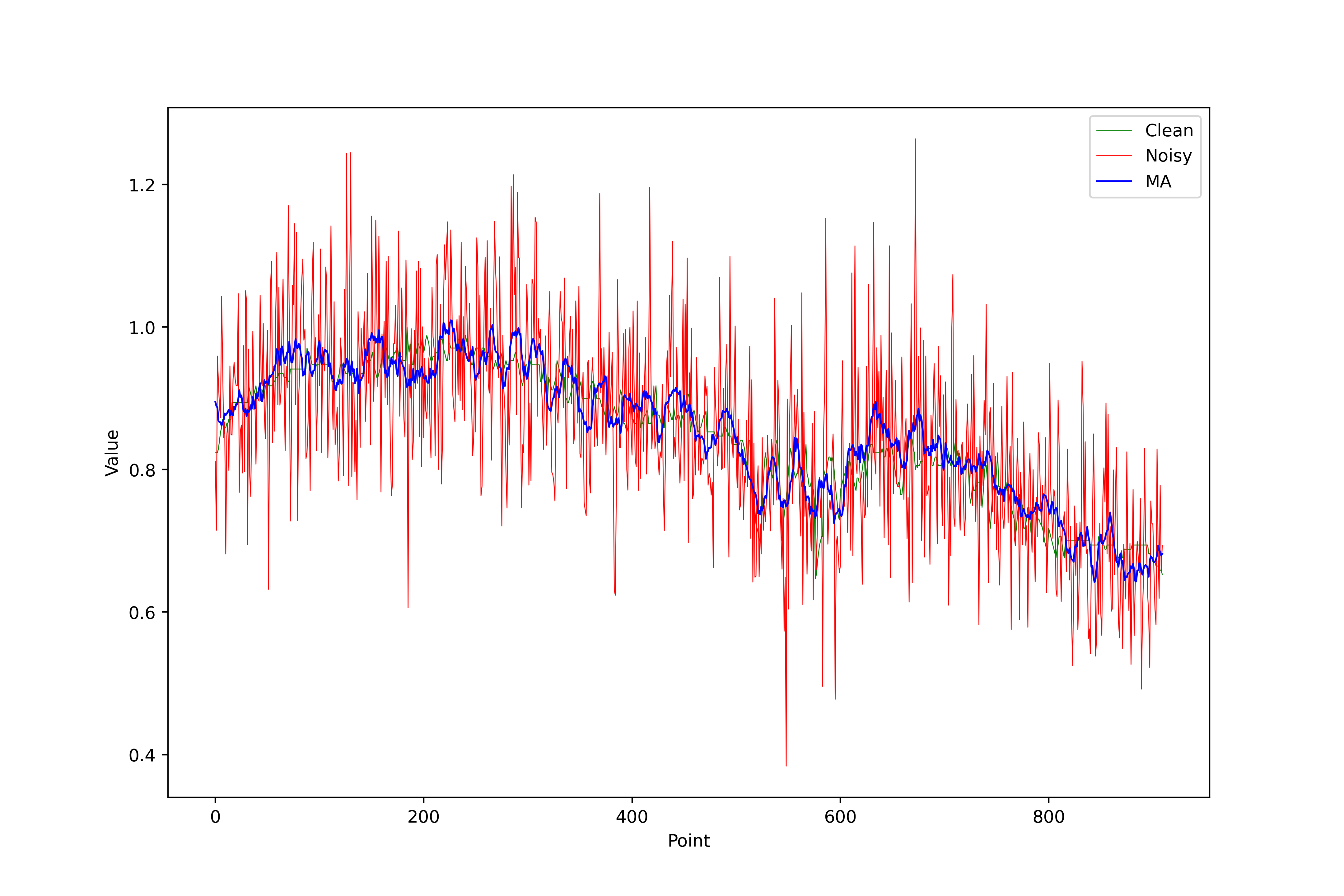
Moving Average

Averages values in symmetric windows.

Equation: \(y[i] = \frac{1}{N} \sum_{k=-w}^{w} x[i + k]\) where ( N = 2w + 1 ) (window size).

Parameters:

Filtered Results: MA_CMajor MA_profile

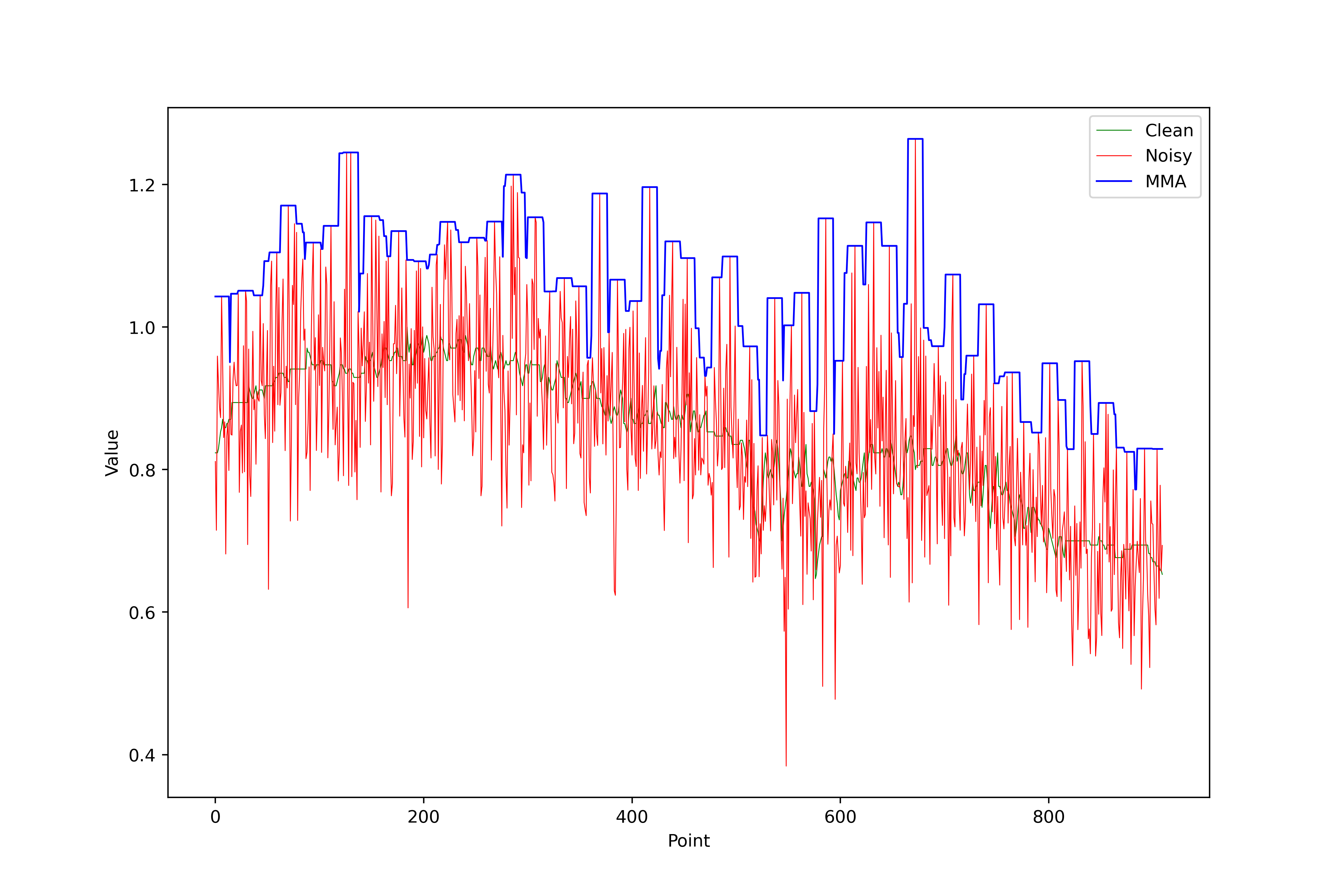
Moving Maximum/Minimum

Upper envelope (maximum) or lower envelope (minimum).

Equation (maximum): \(y[i] = \max \{ x[i - w], \ ..., \ x[i + w] \}\)

Parameters:

Filtered Results (maximum): MMA_CMajor MMA_profile

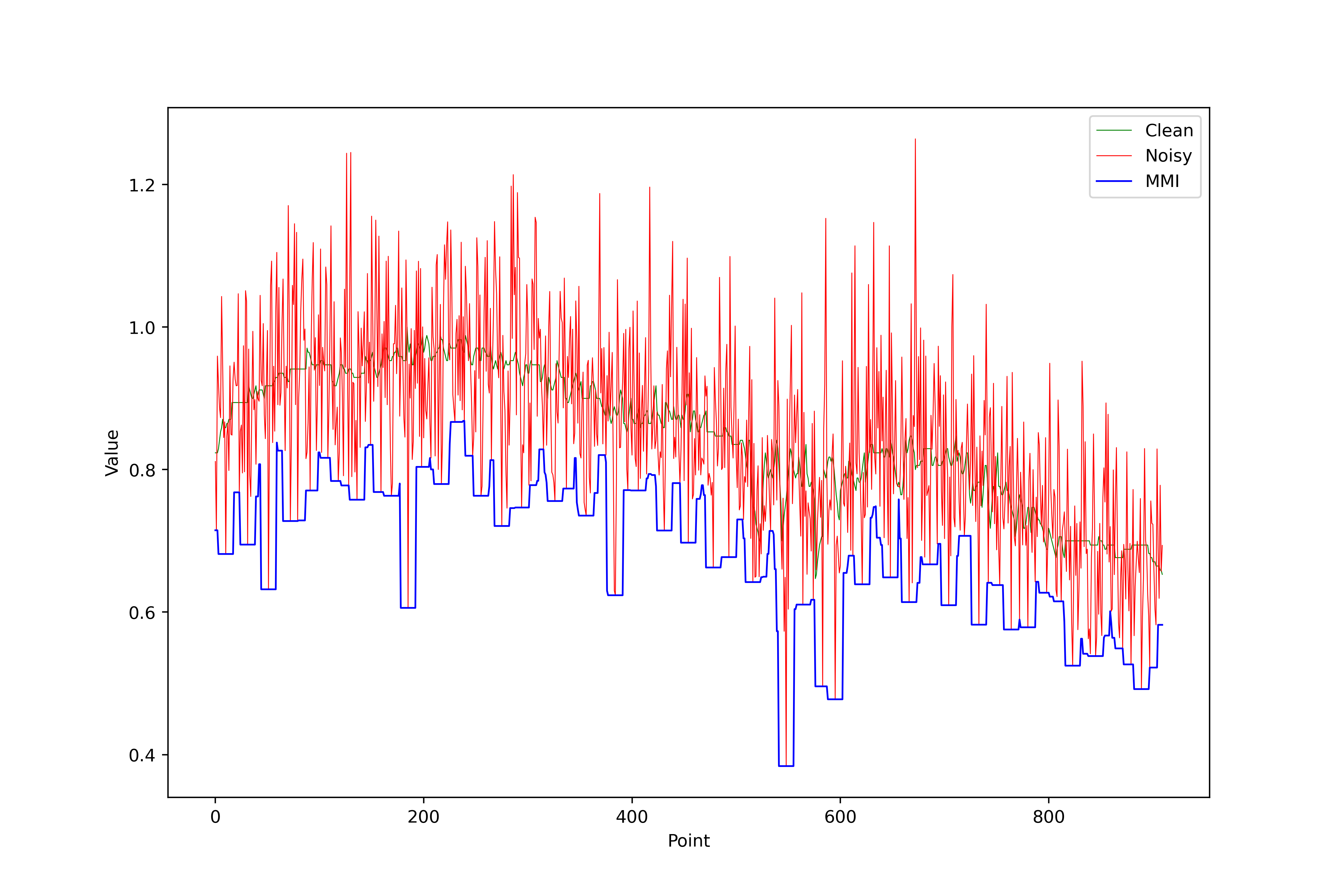
Filtered Results (minimum): MMI_CMajor MMI_profile

Moving Median

Removes outliers using local median.

Equation: \(y[i] = \text{median} \{ x[i - w], \ ..., \ x[i + w] \}\)

Parameters:

Filtered Results: MM_CMajor MM_profile

L0 Gradient Minimization

Promotes constant regions (zero gradients).

Energy Equation: \(E(u) = \|\nabla u\|_0 + \lambda \|u - f\|_2^2\) where ( |\nabla u|_0 ) counts non-zero gradients.

Parameters:

Filtered Results: L0_CMajor L0_profile

Hampel Filter

Detects outliers using median and MAD (Median Absolute Deviation).

Decision Equation: \(y[i] = \begin{cases} x[i], & \text{if } |x[i] - \text{median}(W)| \leq \kappa \cdot \text{MAD}(W) \\ \text{median}(W), & \text{otherwise} \end{cases}\)

Parameters:

Filtered Results: H_CMajor H_profile

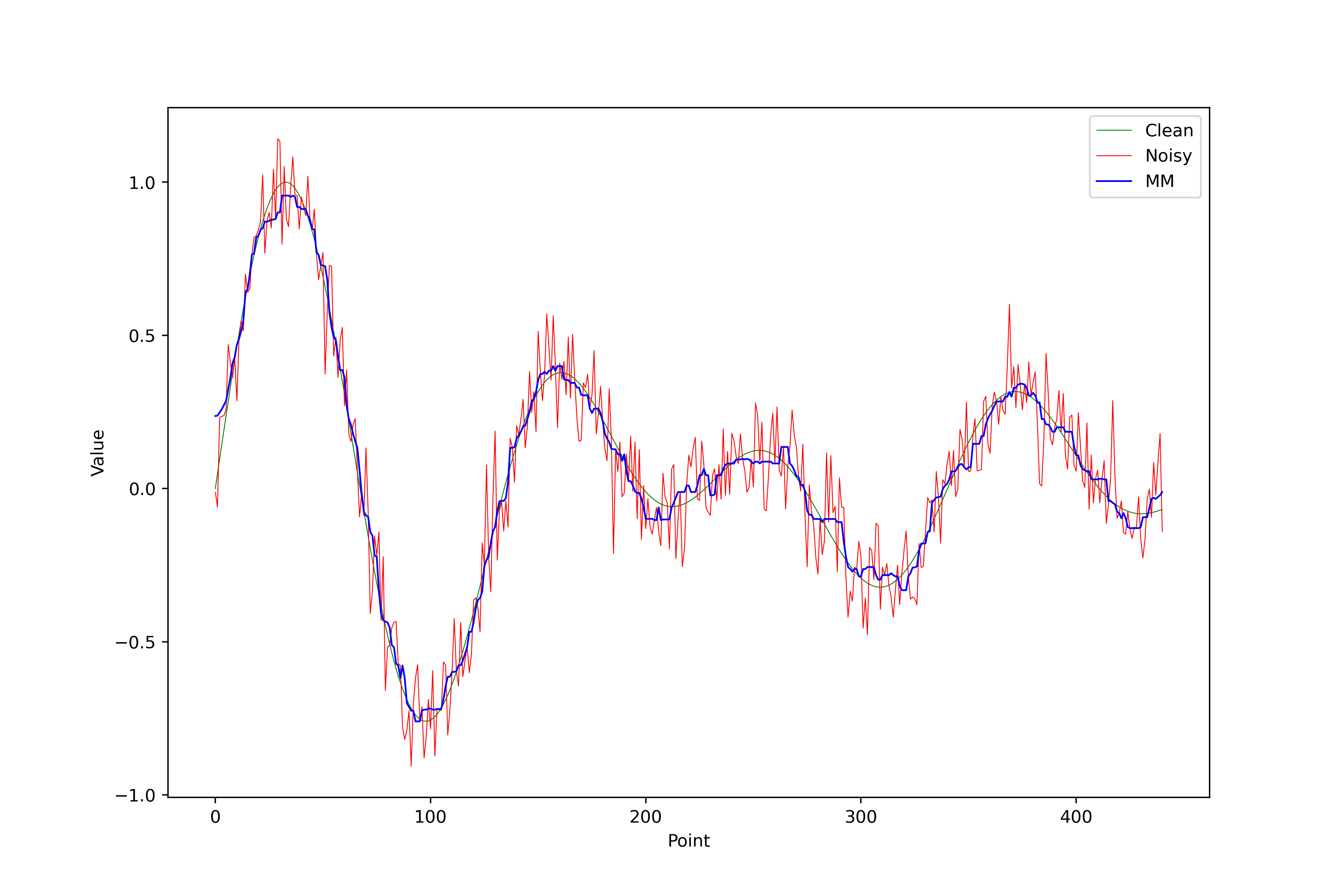
Hampel Variant Filter

Optimized Hampel version approximating MAD using secondary median filter. See the official paper for this filter.

Decision Equation: \(y_t = \begin{cases} x_t, & \text{if } |x_t - m_t| \leq t \cdot S_{t_m} \\ m_t, & \text{otherwise} \end{cases}\) where:

Parameters:

Advantages:

Filtered Results: HV_CMajor HV_profile

Comparison

Some methods aren’t designed for denoising, making universal quality metrics less meaningful. However, we apply PSNR/MSE to core methods: Moving Average, Moving Median, Hampel, Hampel Variant, TV, L0, and Exponential.

MSE (Mean Squared Error)

\(\text{MSE} = \frac{1}{N} \sum_{i=1}^N (y[i] - \hat{y}[i])^2\)

PSNR (Peak Signal-to-Noise Ratio)

\(\text{PSNR} = 10 \cdot \log_{10} \left( \frac{\max(y)^2}{\text{MSE}} \right),\)

where \(\max(y)\) is signal peak value (e.g., 1 for normalized signals).

Noise Model

Our mathematical noise model combines:

Noise and spikes are added via:

std::vector<double> addNoiseAndSpikes(const std::vector<double>& clean_signal, double noise_level = 0.1, double spike_probability = 0.01, double spike_amplitude_max = 0.5) {
    std::vector<double> noisy_signal = clean_signal;  // Copy clean signal
    std::default_random_engine generator;
    std::normal_distribution<double> noise(0.0, noise_level);
    std::uniform_real_distribution<double> spike_prob_dist(0.0, 1.0);
    std::uniform_real_distribution<double> spike_amplitude_dist(0.0, spike_amplitude_max);

    for (size_t i = 0; i < clean_signal.size(); ++i) {
        noisy_signal[i] += noise(generator);  // Add Gaussian noise
        if (spike_prob_dist(generator) < spike_probability) {  // Add spike
            double spike_amplitude = spike_amplitude_dist(generator);
            noisy_signal[i] += spike_amplitude;
        }
    }
    return noisy_signal;
}

The additive noise model (apart from the non-linear noise inherent to the profile scan) is:

\[y_i = x_i + \eta_i + s_i,\]

where:

Results

We test methods on a C Major chord signal and a real laser-scanned profile.

C Major Chord

A C Major chord combines frequencies:

Note Frequency (Hz)
C 261.63
E 329.62
G 392.00

Generated in C++ as:

std::vector<double> generateChordSignal(double duration_ms, double sample_rate = 44100.0) {
    int size = static_cast<int>((duration_ms / 1000.0) * sample_rate);
    double freq_C = 261.63, freq_E = 329.63, freq_G = 392.00;
    std::vector<double> signal(size);
    
    for (int i = 0; i < size; ++i) {
        double t = i / sample_rate;
        signal[i] = std::sin(2*M_PI*freq_C*t) + std::sin(2*M_PI*freq_E*t) + std::sin(2*M_PI*freq_G*t);
    }
    return signal;
}

Clean vs. noisy 10ms signal:

signal_CMaj

Audio Samples:

Quantitative Comparison

Method PSNR (dB) MSE
Moving Average 29.927 0.001017
Moving Median 27.9873 0.001590
Hampel 27.6265 0.001727
Hampel Variant 27.8575 0.001638
TV 27.477 0.001788
L0 18.6888 0.013525
Exponential 23.2828 0.004696

Not so surprisingly, the best method (under these highly controlled conditions) is the Moving Average. This is due, besides the synthetic and ideal nature of the noise added to the synthetic signal, to the inherently “smooth” nature of the sum of sines. It is well known that the mean norm promotes smooth solutions and “eliminates” any sharp features in the signal, similar to L2 norm-based regularizers. However, this is usually not desirable in real-world applications. Filters such as the Hampel variant manage to be robust against outliers and achieve a good reconstruction result compared to other filters.

Laser Profile

Noisy laser profile (additional synthetic noise added):

signal_profile

The visual filtering results are shown in their respective sections. Since we lack ground-truth data for this signal, traditional metrics like PSNR aren’t applicable, but we could evaluate the filtering quality through ‘unsupervised’ (talking in ML argot) approaches such as Stein’s risk estimators, entropy analysis, or noise stationarity measurements. A proper evaluation would need to consider both noise suppression and feature preservation characteristics specific to our profilometry application, leaving this as valuable future work requiring careful methodological development.

Conclusion

Parameter tuning is critical for optimal performance. Methods with fewer parameters (e.g., Moving Average) offer practicality but may lack flexibility for highly degraded signals. TV/L0 priors favor piece-wise constant solutions, making them suitable for step-like signals (e.g., TTL pulses) but less ideal for smooth signals. The exponential filter introduces inherent delay, useful for prediction but suboptimal for denoising. A detailed case study is needed to bound each method’s capabilities under varying degradation types/levels.

References

TODO